4. Binomiális eloszlás

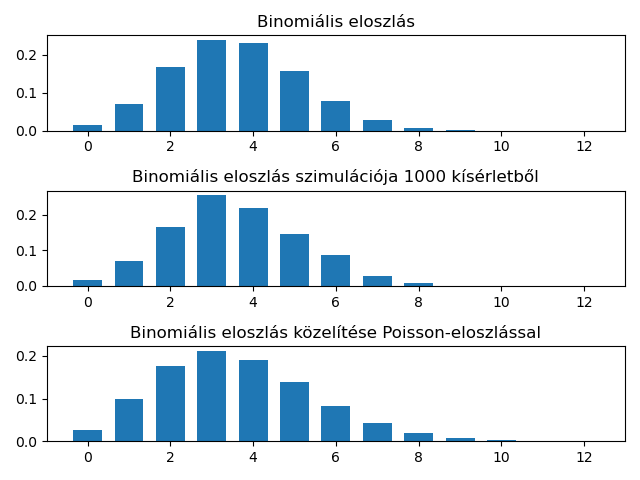
E feladatban három oszlopdiagramot kell kirajzolni egyetlen ábrában, minden részábra fölött egy-egy címmel. Az első ábra egy \((n,p)\) paraméterű binomiális eloszlás valószínűségeloszlását mutatja (címe „Binomiális eloszlás”), a második ábra e binomiális eloszlást szimulálva tapasztalati valószínűségeloszlást mutat (címe „Binomiális eloszlás szimulációja 1000 kísérletből”), míg a harmadik ábra a binomiális eloszlást közelítő \(\lambda=n\cdot p\) paraméterű Poisson-eloszlás valószínűségeloszlásának első \(n+1\) oszlopát ábrázolja (címe „Binomiális eloszlás közelítése Poisson-eloszlással”).

A program eredményeként valami hasonló ábrát fogunk kapni (a színek, skálázás,... nem lényeges része a feladatnak):

A program bemenete \(n\), \(p\), \(k\), ahol \(n\) és \(p\) a binomiális eloszlás paraméterei, és \(k\) a szimulációk száma. A fájl neve legyen binom.py és parancssorból legyen így indítható:

python3 binom.py 12 0.3 1000

• A pontozás miatt a main() függvény adja vissza a használt pyplot típusú objektumot, például így

  import matplotlib.pyplot as plt
  
  ...
  
  def main():
      fig = plt.figure(figsize=(10, 5))
  
      ...
  
      return fig
  
  if __name__ == "__main__":
      main()
  

• A parancssori argumentumok lekérdezhetőek a beépített sys.argv tömbben, ami a következő 3-soros mintaprogrammal kipróbálható:

  import sys
  
  print(f'n: {sys.argv[1]}, p: {sys.argv[2]}, k: {sys.argv[3]}.')
  print(f"E program neve {len(sys.argv[0]):2} betűből áll.")
  

• Ne felejtsük el, hogy a sys.argv[1] stb. paraméterek karakterláncok, ezért konvertálni kell őket számokká (int, float). A kész programot futtassuk le különböző számhármasokon, pl. 20 0.05 1000, 40 0.02 1000, 40 .5 1000.

• A binomiális eloszlás szimulációja megvalósítható úgy, hogy \(n\) kísérletet végzünk egy \(p\) valószínűségű esemény bekövetkezéseinek számára. A valószínűségi változó értéke \(m\), ha az esemény az \(n\) kísérletből \(m\)-szer következett be. Ezt az \(n\) kísérletet \(k\)-szor megismételjük, így a valószínűségi változó \(k\) darab értékét kapjuk. A második diagram \(m\)-edik oszlopa \(i/k\) magas legyen, ha a valószínűségi változó \(i\)-szer vette föl az \(m\) értéket. (A feladat e pontja egyszerű ciklusokkal és a random modul random függvényével megvalósítható.

• A harmadik ábra egy Poisson-eloszlású \(X\) valószínűségi változó első \(n+1\) értékét mutatja, ahol \[ \mathbb{P}(X=m)=\frac{\lambda^m}{m!}e^{-\lambda}, \quad m=0, 1, 2,\dots,\] ahol \(\lambda=np\).

• A feladat célja binomiális eloszlású valószínűségi változó szimulálása, Poisson-eloszlásúval való közelítése, és ezeknek az elméleti eloszlással való összehasonlítása.

• Programozási célok: program parancssorból való indítása, paraméterek átadása parancssorból, oszlopdiagram és részábra kirajzolása, véletlen események szimulálása.