6. Bertrand-paradoxon

• A Bertrand-paradoxon (valójában nem paradoxon) arra példa, hogy egy látszólag egyszerű valószínűségi változó milyen sokféleképp valósítható meg, ha a definíciója nem elég egyértelmű. E paradoxon klasszikus változata azt kéri, hogy számítsuk ki annak valószínűségét, hogy egy adott körbe véletlenül berajzolt húr mekkora valószínűséggel lesz rövidebb, mint a körbe rajzolható egyenlő oldalú háromszög oldala (ld. Wikipédia). Paradoxonnak azért tűnik e probléma, mert három különböző, egyaránt józan feltevés mellett az \(1/2\), a \(2 / 3\) és a \(3 / 4\) is helyes válasz lehet.
  1. Az első feltevés az, hogy választunk egy véletlen irányt (ez szimmetria okokból lehet bármelyik, így akár a vízszintes is) és a húrt a rá merőlegesek közül választjuk ki, véletlenül választva egy pontot a kör vízszintes átmérőjén.
  2. A második feltevés az, hogy választunk a kör kerületén egy pontot és a húr másik végpontja a kör kerületének egy másik, véletlenül választott pontja lesz.
  3. A harmadik feltevés az, hogy választunk a körlapon (egyenletes eloszlás szerint) egy pontot, és azon keresztül húzunk egy húrt úgy, hogy az merőleges legyen a pontot a középponttal összekötő egyenesre.

  Mindhárom feltevést és a megoldást is (kicsit más megfogalmazásban) ötletes és élvezetes animációkkal szemlélteti az MIT egy oldala (a megoldás elolvasása előtt érdemes kicsit töprengeni rajta!)

  A továbbiakban legyen a kör egységsugarú, tehát az átmérője \(2\), és jelölje a húr hosszát egy kísérletben \(X\), azaz \(X\) egy valószínűségi változó, melynek értéke \(0\) és \(2\) közé esik. A feladat az lesz, hogy írjunk egy programot, mely mindhárom modellben szimulál \(N\) kísérletet a húr kiválasztására, följegyzi a hosszakat egy listába, és annak alapján kirajzolja mindhárom esetben a tapasztalati eloszlásfüggvényt. A tapasztalati eloszlásfüggvény értéke az \(x\) helyen azt mondja meg, hogy mennyi a relatív gyakorisága az eseménynek. E függvény lépcsős függvény. (Az eloszlásfüggvényt becsüljük vele, melynek definíciója \(F_X(x)=P(\{X < x\})\).) Ha például három kísérletet végezve a húrok hossza \(1.5\), \(0.4\) és \(1.2\), akkor a tapasztalati eloszlásfüggvény ábrája így néz ki (ha azt a matplotlib.pyplot grafikai könyvtár step függvényével rajzoljuk; tekintsünk el a lépcsős függvénybe berajzolt függőleges szakaszoktól, és a szakadási helyeken gondoljuk a lépcsős függvényt balról folytonosnak):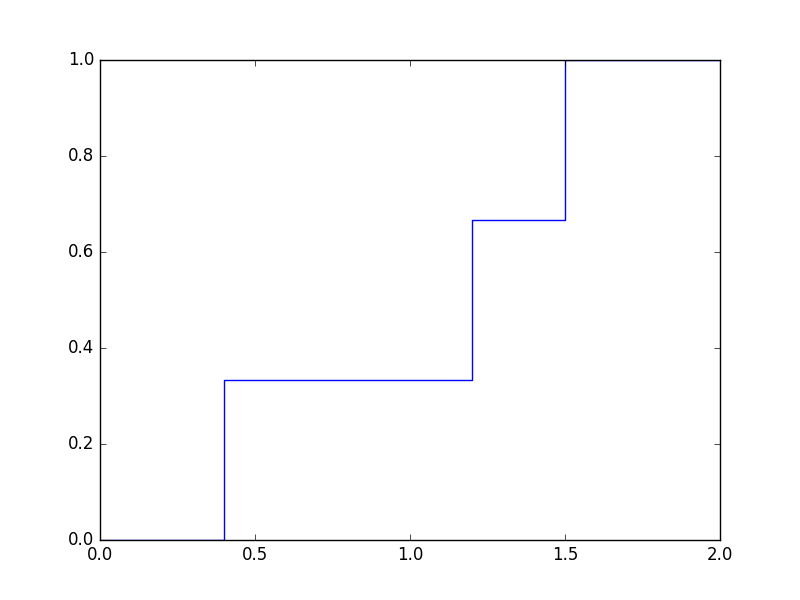
  

  A három modellt az itt elérhető fájlban kell megvalósítani, a program kimenete legyen a három tapasztalati eloszlásfüggvény grafikonja egyetlen ábrán. A függvényeket elég a \([0,2]\) intervallum fölött ábrázolni. Nyilván mindhárom függvény monoton növekvő, értéke \(0\)-ban \(0\),\(2\)-ben \(1\), és a paradoxon megoldásából tudjuk, hogy \(\sqrt{3} \approx 1.732\) helyen közelítőleg \(1/2\), \(2/3\), illetve \(3/4\) a modelltől függően.

• Megvalósítás:
  • Az első modellhez: válasszunk egy véletlen \(r\) számot és számítsuk ki az \((r,0)\) pontba állított, \(x\)-tengelyre merőleges húr hosszát (ehhez a math modul acos és sin függvényeit használjuk).
  • A második modellhez: legyen az egyik pont az \(1,0\), a másik pont legyen a kör kerületének egy véletlen pontja, azaz \( \cos \alpha, \sin \alpha\), ahol \(\alpha\)-t válasszuk egyenletes eloszlás szerint a \([0, 2 \pi )\) intervallumból (itt ki kell számítani e két pont távolságát).
  • A harmadik modellhez: válasszunk először egy tetszőleges pontot a \([-1,1] \times [-1,1] \) négyzetből (azaz válasszunk két véletlen számot a \([-1,1]\) intervallumból, és képezzünk belőlük számpárt), és ellenőrizzük, hogy a körbe esik-e. Ha nem, válasszunk még egyet addig, míg egy körbe esőt nem találunk. Ha találtunk, az origótól való távolságából az első modellhez hasonlóan számolható a húr hossza.
  • A tapasztalati eloszlásfüggvény kirajzolásához: ha szimuláltunk \(N\) kísérletet, egy sort() metódussal rendezzük, írjunk az elejére egy \(0\)-t, végére egy \(2\)-est. Ez a lista adja a rajz vízszintes tengelyén a beosztásokat, amely pontok felett a lépcsős függvény „ugrik”. Minden egyes ilyen helyen a függvény értéke \(1/N\)-el nő. Ha alegrövidebb húr hossza \(r\) (ez \(1\) valószínűséggel nagyobb \(0\)-nál), akkor a függvény a \([0,r]\) intervallumon 0, így a függvényértékek listáját érdemes \([0,0,1/N,2/N\dots,1]\)-nek választani. A kirajzoláshoz a program a matplotlib.pyplot.step(x,y) függvényt használja, ahol \(x\) és \(y\) az előbb konstruált két lista. (E Python függvény a grafikonba függőleges vonalakat is berajzol.) Egy megoldást mutat a következő ábra \(N = 1000\) esetén
    
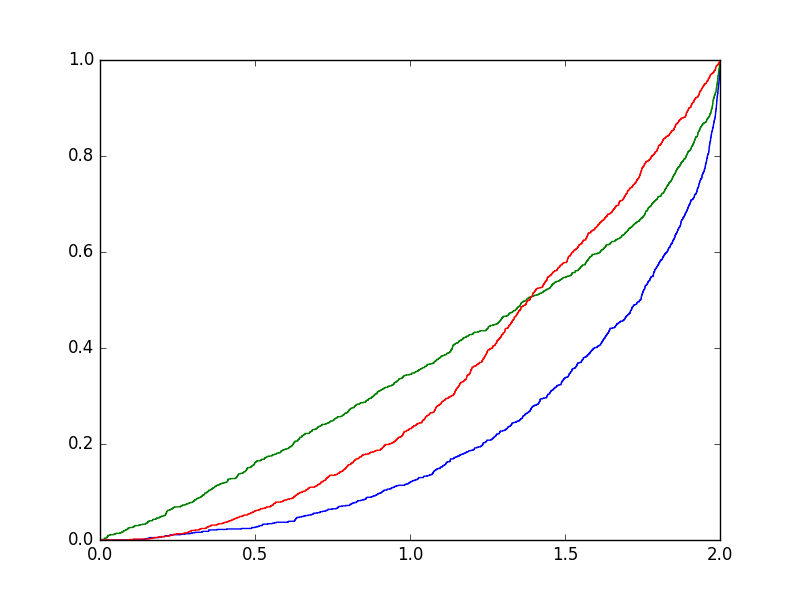
  • A program elkészülte után végezzünk kísérleteket különböző \(N\) értékekkel.
  • A feltöltendő fájl neve is legyen Bertrand.py és legyen terminálból hívható, ahol az \(N\) értéke átadható. Például \(N = 100 \) esetén legyen a parancs
    

      python3 Bertrand.py 100
    

• A feladat célja a következő fogalmak megértésének elősegítése: folytonos valószínűségi változó, eloszlásfüggvény és annak tapasztalati közelítése.
• Programozási szempontból a feladat nem tartalmaz új elemeket, célja az eddig megszerzett ismeretek gyakorlása.